计算机安全：蒙哥马利约减

蒙哥马利约减

目前使用最广泛的模指数运算方法

问题

求y mod N，N为质数。y称为x模N关于R的Montgomery约减,即y=xR’ mod N

附加条件：不使用除法（除法速度慢）

尽量避免使用取模运算
用移位、减法运算替代取模运算

设计

1.取R为2的n次方(如果 N表示为n个b进制数，则 R取b的幂次方)，这样/ R即右移，*R即左移，mod R即与（R-1）按位与，大大提高了速度。

2.N<R,R和N互质，即存在R’和N’，使得RR’ + NN’＝1(保证对任意的x＜R，有k＜R，使得kN=x＜R。这保证表达式(见下文)的后半部分有解，且大小不超过R/R=1)。同时，加上y/R＜N，故表达式的前半部分大小不超过N。综上可得，表达式整体大小不超过2N(故取模可以用减法做)。

推导

设T=Qm+r，欲求T mod m
将T分为n的两部分，高n位为T’，低n位为T’’
则：$$\frac{T}{R}modm=T^{\prime }modm+0.T^{″}modm$$
前半部分只需要移位和最多一次减法。
对于后半部分，需要找到0.km，使其与表达式后半部分相加，能将小数部分变成0。即T’’+km=cR(R的低位全为0)。加之m和R互素，故这样的k一定存在。实际上，k=-1/m*T’’ mod R
综合可得，T+km是R的倍数。

结论

$$(x-(x\ast N\prime modR)\ast N)/R\equiv x\ast R^{\prime }modN$$

$$(x-(x\ast N\prime modR)\ast N)/R<2R$$

x模 N 关于 R 的Montgomery 约减用2次乘法、1次加法(把-k换成k)、2次移位、1次减法(最后取模时使用)。
注意：xmod R和x’’ modR结果一致，因为x’mod R结果为0。同时，结论的x*N‘ modR等于推导式中的-k

例子

取N = 3457，R = 2^16，得到N’＝12929，R’＝682。求y mod N：

计算得$$3310\equiv RmodN$$

由结论得，$$y\equiv (y\ast R-(y\ast R)\ast N\prime modR\ast N)/R$$

代入计算得，$$y\equiv (y\ast 3310-y\ast 3310\ast 12929mod{2}^{16}\ast 3457)/2^{16}$$

这种方法的另一个优势在于，$$R\ast N\prime modR\ast N$$也即$$12929mod{2}^{16}\ast 3457$$ 可提前计算。

函数

int f(int a)
{
int t;
int u;
    u = a * QINV;  //QINV固定
    t = u * CTRU_Q;//CTRU_Q固定
    t = a - t;
    t >>= 16;
    return t;
}

应用：模指数

计算 $$x^{5}modm$$

计算x*R²的M约减 $$x̃=xRmodm$$

计算x̃²的M约减A： $$x{̃}^2/Rmodm$$

计算A平方的M约减 $$A^2/Rmodm=x{̃}^4/R^{3}modm$$

A平方的M约减 乘 x̃的M约减，再进行约减，即得。

乘方写成函数如下：

x̃ = MR(x * (R方 mod m)), ã = MR(1*(R方 mod m) ) //逆向快速幂，输出：x^{e} mod m.
For i = t downto 0
ã = MR(ã* ã)
If ei = 1 then ã = MR(ã* x̃)
a = MR(ã)
Return(a)

应用：取模乘法

计算 $$c=x\ast ymodm$$

计算x的M变换 $$x^{\prime }=x\ast 2^{n}modm$$

计算y的M变换 $$y^{\prime }=y\ast 2^{n}modm$$

计算x’和y’的积，再进行M约减 $$c^{\prime }=x^{\prime }\ast y^{\prime }/2^{n}modm$$

进行约减，即得。

优化：用M约减实现M变换

即计算$$x^{\prime }=x\ast 2^{2n}/2^{n}modm$$

优化：多精度M约减

当T比较大时。
T为2n位，N为n位，R为b的n次方。
理论：

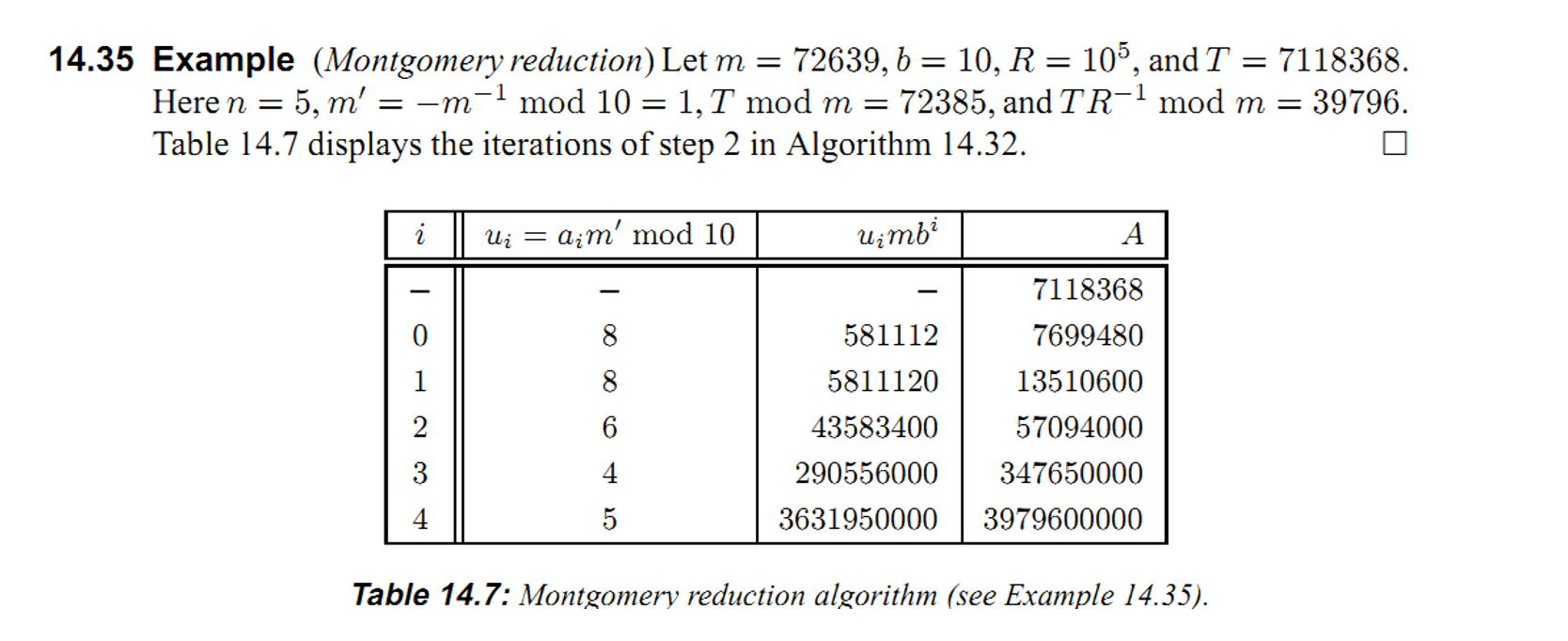
实例：

优化：多精度M乘法

x为n位，y为n位，N为n位，R为b的n次方。
理论：

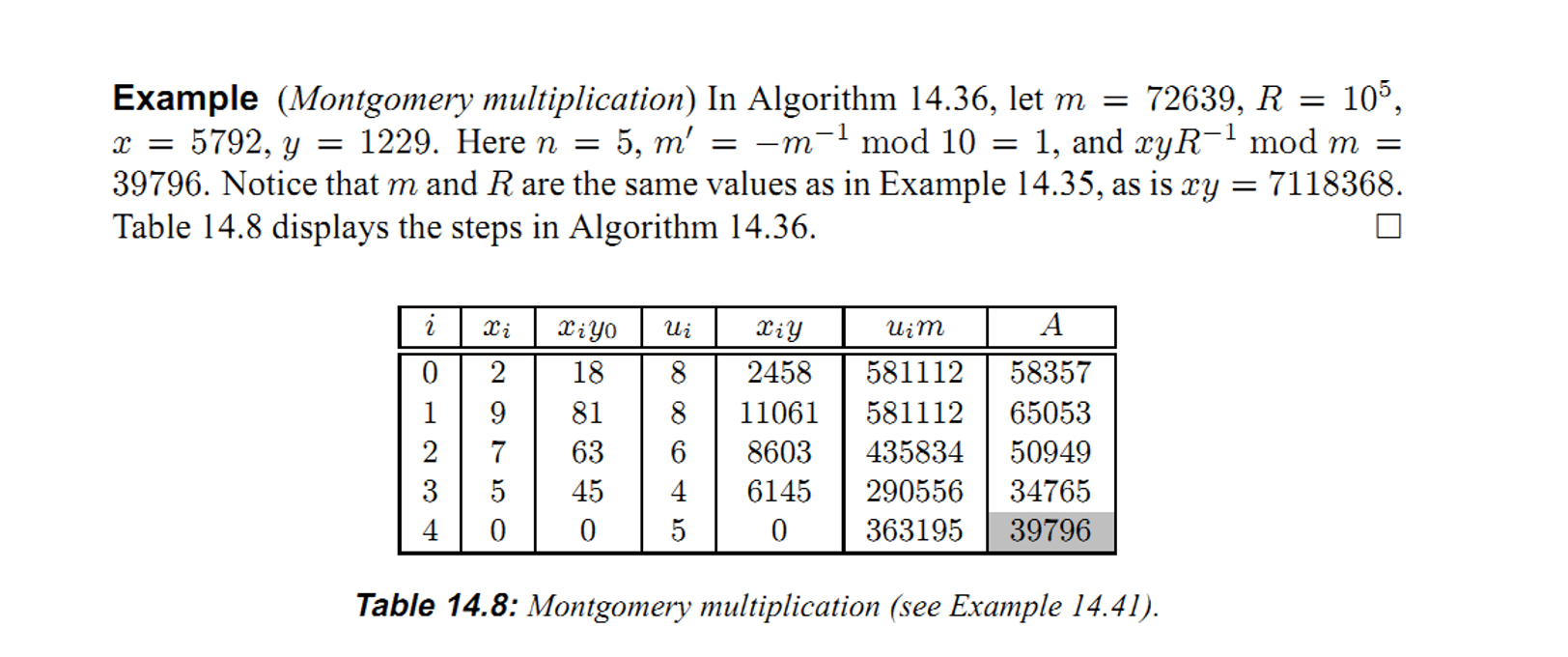
实例：

证明方式见回放

barrett约减

其中r1-r2可能为负数，只需要加一次模。(因为−b^{k+1} < r1 − r2 < b^{k+1})
其中第四步最多执行2次。(因为Q-q3≤2)
设x=Qm+r，则x 的高 k+1位与 1/m 的高 2k 比特中的低 k+1 位相乘，取整数部分(高k+1位)得到Q的近似值q3(Q-2≤q3≤Q)。Qm+r-q3m对m取模得到r。
问题
为什么是模b的k+1次方，为什么要求b>3？ Click 因为r1-r2＜3m，而m占据k位，如果需要r1-r2少于k+1位(极致地压低模的大小有利于计算速度)，则b>3。若b≤3，则r1-r2为负数时，不只需要加一次模。b的k+1次方，是能保证正确性下的，最方便计算的模数。
为什么r1和r2对非m取模，不影响正确性？ Click 若m＝1，则结果为1；若m=2，则判断奇偶性；m≥3时，因为Q-q3≤2，且b的k+1次方大于2，故r1、r2对b的k+1次方取模后相减，不会影响正确的Q和q3的差值。加之r＜m＜b的k+1次方，故不会影响正确的r的大小。 实际上，我们并不需要关心Q和q3相差了多少和变没变。这个结果无非是m的系数，多减几次m便可以去除。但是，将Q-q3的结果控制在固定大小内，可以优化减m的速度。
为什么要求b>k？ Click 使q2的 k − 1位的进位最多是1，若 b 远大于 k，则只需包括 k 和 k+1位的计算。 q2 的低 k-1 位不用参与计算。**详细证明见回放**

例子

$$b=4,k=3,x=(313221{)}_b,m=(233{)}_b(x={3561}_{10}，m={47}_{10}).$$

$$\frac{1}{m}=(0.00111302···{)}_b⟹\mu =\lfloor \frac{4^6}{m}\rfloor =(1113{)}_b,$$

$$x=(313221{)}_b⟹q1=\lfloor \frac{x}{4^2}\rfloor =(3132{)}_b,$$

$$q2=\mu ·q1=(10231302{)}_b⟹q3=(1023{)}_b$$

$$x=(313221{)}_b⟹r1=(3221{)}_b$$

$$q3·m=(313011{)}_b⟹r2=(3011{)}_b,$$

$$r=r1-r2=(210{)}_b$$

故 x mod m = 36。

参考：
1.CSDN：蒙哥马利约减
2.CSDN：Montgomery reduction——多精度模乘法运算算法