cs保研经验贴|高等数学
可微、连续、可导
可微:设函数在P的领域内有定义,如果全增量deitaZ=Adeitax+Bdeitay+o(p),其中A,B是不依赖deitax,deitay的常数,则称呼z在P点可微,Adeitax+Bdeitay为P点的全微分。
导数:描述的是某点切线的斜率。
极限:去心领域内有定义
微分:描述的是一点的函数值的增量,且该增量是自变量与一个和自变量无关的常数的乘积,含义为用一条线性函数在某点逼近原函数。相较于导数,微分更具有直接的形式,能够更方便地解决微分方程、进行积分,并扩展到多元的情况。
连续:
一元函数:可微和可导等价;可导必连续,连续不一定可导(狄利克雷函数,处处连续,处处不可导);连续必可积,可积不一定连续
多元函数:偏导连续一定可微,可微一定连续、偏导存在;连续不一定可微;连续必可积,可积不一定连续
有四则运算法则、求导/偏导/微分的链式法则(需要分清哪些是自变量、中间变量)。
一阶导数/全微分的形式不变性:无论被求导/全微分的变量是自变量还是中间变量,最后的形式相同。
中值定理
条件:闭区间连续,开区间可导。
(1)罗尔定理:往复运动必有一时刻速度为0;
(2)拉格朗日中值定理:物体从一个地方移至另一个地方的过程中,必有一时刻加速度为0;
(3)柯西中值定理:一段曲线运动过程中,必有一点的切线斜率,等于两端点的割线的斜率,即速度与位移方向相同。
洛必达法则
在x0的领域内有定义、且极限为0比0或无穷比无穷型、同时在x0的去心领域内可导且分母的导数不为0。
函数极值与极限
不可导点、驻点统称为可能极值点。
函数极限、数列极限的性质:极限唯一性、f(x)在x0去心领域有界、保号性。
三大公式
格林公式:沟通了沿闭曲线的曲线积分与曲线所围区域上的二重积分之间的联系,将曲线积分转化成二重积分求解。
高斯公式:建立了沿空间封闭曲面的曲面积分与曲面所围区域的三重积分之间的联系,将曲面积分转化为三重积分求解。
斯托克斯公式:将三维上的曲线积分转化为曲面积分求解,它是格林公式的一般情形。
梯度:一个向量,表示一个标量场在某一点处的最大变化率及变化的方向。
高斯公式:通过一个闭合曲面的通量等于该曲面内部的散度的积分。
散度:一个数,指单位体积内所产生或吸收的通量,反映向量场发散程度。
斯托克斯公式:沿着闭合曲线的环流等于该曲线所围成的曲面上的旋度的通量。
旋度:一个向量,表示一个向量场在某一点的旋转趋势,和向量场的环流量有关。
曲率:当弧长趋于0时,切线转角的大小与弧长比值的极限即为曲率。
曲面积分和二重积分等
二重积分是在二维平面上对某个区域D上的二元函数f(x, y)进行积分的过程。第一类曲面积分的积分区域是三维的曲面。第二类曲面积分再加上方向。
第一型曲线积分:是对弧长的曲线积分,曲线长度、面积。计算方法:利用参数方程的公式转换。
第二型曲线积分:是分别对坐标x,y 的曲线积分,变力沿曲线做的功,积分下限不需小于积分上限。计算:第二型转第一型(利用方向余弦),第一型转一次积分。
两类曲线积分之间的联系,可以通过方向余弦联系起来。
第一型曲面积分:面积、体积。计算:利用参数方程的公式转换。是在三维空间里的对面积的曲面积分。
第二型曲面积分:流体流向曲面一侧的流量,对坐标平面积分。计算:分面投影法、合一投影法为二重积分;用方向余弦转为第一型曲面积分。
二重积分计算方法:将积分区域D划分为x型域或y型域,再二次积分;二次积分也能借用二重积分为中转,进行换序以简化运算。
三重积分计算方法:先一后二法(先算一次积分,再算xy域的二重积分)、先二后一法、三次积分法、柱坐标法、球坐标法、换元法(利用雅可比行列式)。
二重极限:当函数在一个点的去心领域内有定义,自变量x,y同时、无论路径地趋近一个点时,函数值趋近一个常数A。二次极限:分步骤趋近,两个二次极限未必相等。但二重极限、二次极限都存在时,必相等。
连续:
一致连续:不论在区间中的任何部分,只要两个自变量的数值接近到一定程度,就能使它们对应的函数值达到所指定的接近程度。
一致收敛:…
收敛:
闭区间上,一致收敛和收敛等价,连续和一致连续等价。
梯度、方向导数
方向导数:是一个数;反映的是f(x,y)在P0点沿方向v的变化率。
导数:描述的是一个极限,即当自变量的增量趋近0时,函数值的增量与自变量的增量的比值,含义为某点的变化率。
偏导数:是多个数(每元有一个);是指多元函数沿坐标轴方向的方向导数。
梯度:指函数值增长最快的方向。
偏导数连续才有梯度存在。
梯度可用于求法向量/法平面,进行梯度下降优化(最小化损失函数)。
泰勒级数与泰勒公式
泰勒多项式 (Taylor Polynomial)内容: 指泰勒公式/定理中的多项式部分 P_n(x; a)。
“将函数进行泰勒展开”,得到的结果可以是有限阶的泰勒公式/多项式,也可以是无穷的泰勒级数(如果收敛且等于原函数)。
泰勒级数是由泰勒公式中的多项式部分 P_n(x; a) 在 n → ∞ 时形式地取极限得到的。它是泰勒公式/定理的无限延伸。泰勒定理的余项 R_n(x) → 0 (当 n → ∞) 是泰勒级数收敛到 f(x) 的充分必要条件。
具有Lagrange型余项的Taylor公式对于x0点邻域内的任意x都成立,而具有Peano型余项的Taylor公式只对充分靠近xo的x才成立。
反函数
连续性+ 严格单调(单射) ⟹ 反函数存在且连续;
一一映射<—>反函数存在;
积分
积分计算方法:公式法、分步积分法、第一类换元积分法(凑微分法)、第二类换元积分法(变量代换法)、万能代换(有可能使计算复杂化)。
闭连:函数可积、定积分估值定理、积分中值定理。
闭连:积分上限函数可导,存在原函数。
闭有界,有限个第一类间断点:可积。
可积函数分步可积、四则运算可积。
有原函数和可积无关系。可积只和选定区间内被积函数的有界性和连续性有关。
牛顿-莱布尼兹公式将求定积分的问题和求不定积分联系起来,转化为原函数两个值相减。
级数和幂级数
单调有界的数列必收敛,满足夹挤定理的数列收敛。
级数发散;若末项的极限不为0,则发散。
正项级数收敛的充要条件:前n项和数列{Sn}有上界。
正项级数敛散性:比较判别法、比较判别法的极限形式、比值判别法、根值判别法、积分判别法(对于非负递减函数)、利用几何级数和p-级数。
其他:柯西收敛准则、莱布尼兹判别法(交错级数)、M-判别法。
函数级级数一致收敛:和函数在收敛区间内连续、和函数在收敛区间内逐项可积、和函数在收敛区间内逐项可导(可由此求和函数),且收敛半径相同。
求幂级数的收敛域:abel定理——由单点的收敛性求收敛域。
幂级数展开:直接展开、已知展开式的积分、已知展开式的求导。可展开的条件:存在任意阶导数、拉格朗日型余项的极限为0。
傅里叶级数
傅里叶级数展开:函数可积。
傅里叶级数收敛:满足狄利克雷条件,即连续或只有有限个第一类间断点、有限个极值点。
幂级数在中心点附近高精度逼近、傅里叶级数将函数拆解为不同频率的谐波。
奇展开偶展开:展开式不含cosx或sinx。
傅里叶变换:可以处理非周期性信号(一个信号可以看成一个周期性无穷大T->∞的信号)。傅里叶变换将一个信号从时域转换到频域,得到该信号的频谱。
微分方程
特殊:可分离变量微分方程、齐次微分方程、全微分方程(用格林公式解)、可降阶的高阶微分方程(即按步求导)、欧拉方程。
一阶非齐次线性微分方程(常数变易法解决。其中解含有任意常数的为通解,利用初值条件消除任意常数的问题叫做“柯西问题”、特殊的:伯努利方程)
高阶齐次线性微分方程(已知一解,求另一解的置换法、幂级数解法)、高阶非齐次线性微分方程(常数变易法(列出矩阵))
常系数齐次线性微分方程(特征方程法,根据特征根写出通解)、常系数非齐次线性微分方程(待定系数法(不用积分就能求出特解)))
立体几何
平面:点法式方程、三点方程(行列式形式)、一般方程、截距式方程
直线:对称式方程、参数方程、一般方程(联立两平面)








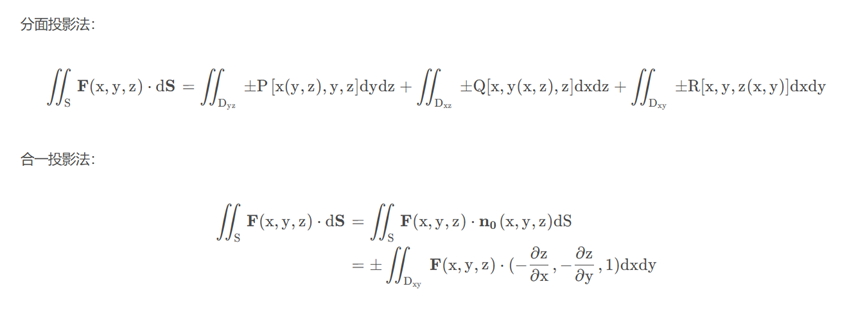



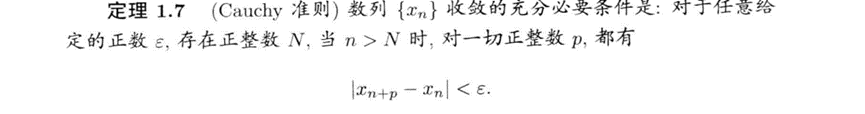
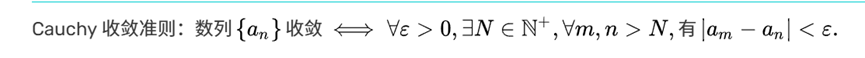


.jpg)
.jpg)
.jpg)
.jpg)
.jpg)