cs保研经验贴|数据结构
数据结构
按某种逻辑关系将一批数据元素组织起来,按一定的存储方式将它们存储起来,并在这些数据元素上定义一个操作集合,就得到了一个特定的数据结构。
数据的逻辑结构
逻辑结构是指数据元素之间的逻辑关系,即从逻辑关系上描述数据。
线性结构:线性表。只有一个始末,每个内节点只有一个前驱和后继。线性表:数组,链表,栈,队列
非线性结构:层次结构(树,叶节点可能有多个)、网状结构(图)、集合。节点可能有0、多个前驱和后继。
数据的存储结构
数据结构在计算机中的表示,也称物理结构。分为:顺序存储、链接存储、散列存储、索引存储。
邻接表:顺序存储的顶点表+链接存储的边链表。邻接表利于找邻接顶点。
数据结构的使用
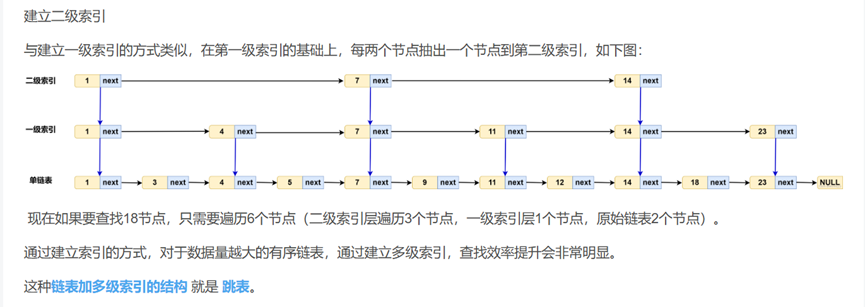
跳表:logn层有序链表,最底层包含所有元素。插入后以1/2递减的概率向上插入,适合动态查找场景。实现方式:四联表。
拉链法很长时,使用红黑树。
哈希表用途:bool过滤器。
树是分层结构,图是网络模型结构;树有根节点,图没有根节点的概念;树的边数为节点数减一,图的边数没有限制;树不能有环,图可以有。
红黑树中的每一个结点的颜色不是黑色就是红色。根结点和所有外部结点(NULL节点、叶节点)的颜色是黑色。红父黑子;所有从根到外部结点的路径上都有相同数的黑色结点数量。对于红黑树查找、插入、删除的最坏时间复杂度为O(logn),最多3次旋转。最长路径的长度是最短路径(仅黑节点)的2倍。任何节点的左右高度最多相差2倍。
自平衡二叉查找树:在平衡度(查找效率)和平衡成本(增删效率)间选择。
简单回路:起点和终点相同,且路劲长度至少为2(三个点)。
同时使用按秩合并、路径压缩,每个操作的均摊复杂度接近O(1)。
AOV网(Activity On Vertex):顶点表示活动或任务(Activity),有向边表示活动(或任务)间的先后关系。应是一个有向无环图(DAG)。拓扑序列:AOV网中所有顶点排成一个线性序列。
AOE网(Activity On Edges):有向边表示活动或任务(Activity), 用边上的权值表示活动的持续时间,顶点称为事件(Event)。求关键活动:先求出事件(点)的最早开始时间和最晚开始时间,再求活动的最早开始时间(等于源点的最早开始时间)和最晚开始时间(等于汇点的最晚开始时间-边长)。
与AVL树相比,红黑树平衡性略弱,故查找效率略低。但插入、删除引起失衡的概率也较小,故插入删除效率更高,维持平衡的成本更低。
时间复杂性
基本运算:算法中起主要作用且费时最多的操作。
时间复杂性:算法中基本运算的次数,往往是问题规模的函数。
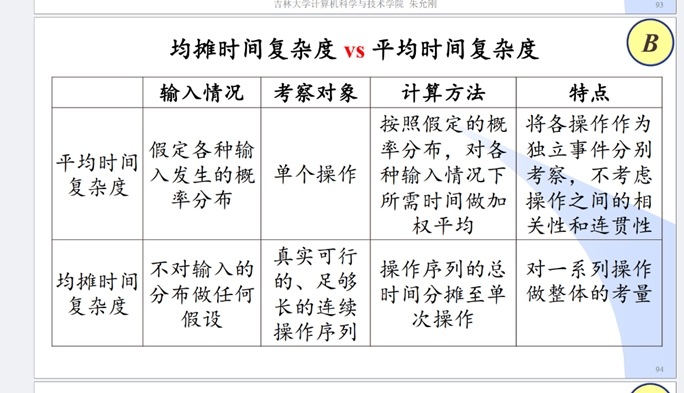
均摊时间复杂度:n次操作的总代价分摊至各操作,均摊时间复杂度考虑了各操作间的关联,且不对输入情况的分布作假设。
栈和队列
栈:进制转换、括号匹配,计算表达式,存储网页浏览顺序、存储函数参数。
中缀表达式转后缀:利用运算符栈:当运算符优先级>栈顶运算符优先级时,压栈。否则,弹栈到栈空、或优先级关系改变、或栈顶为左括号。数字直接压入表达式。
队列:调度度列、缓冲区队列
消除递归
尾递归转循环;
利用栈模拟递归过程;
转为递推关系式。
最短路
dijstla,floyd,A*,bfs,dfs,flod
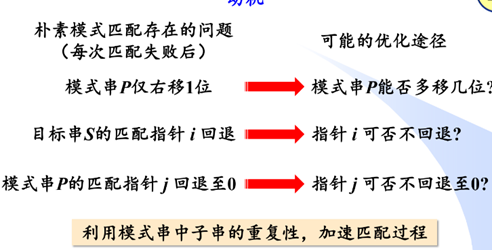
KMP
最小支撑树
最小跨边一定在最小支撑树里。否则,因为支撑树T是连通的,故两个集合间必有一条路径,这条路径一定包含一条跨集合边。
树
树是一种数据结构,它是由n(n>=1)个有限节点组成一个具有层次关系的集合,连通无回路、有n-1条边。
树的存储:顺序存储-孩子表示法、双亲表示法、先根/后根/层次+度表示法、左儿子-右兄弟表示法。
树的应用:哈夫曼树、表达式树、网页与DOM树、语法树、博弈树、并查集。
满二叉树:叶在最后一层、非叶结点都有两个子节点。
完全二叉树:层次顺序下,T的所有节点恰好对应同高的满二叉树的前n个节点。叶子结点只在最后两层、最底层叶子结点都在最左边、有右孩子的前提是有左孩子。非叶节点有n/2个。
线索二叉树:把空指针利用起来,指向前驱或后继。需要增加标志位,来表明是否有左右孩子。中根后继:有右孩子时,为右孩子的中根首节点;否则为将p包含于其左子树的最低祖先。
树转二叉树:1,所有兄弟连线、仅留和左孩子的连线。(右兄弟变右孩子)
二叉树转树:1.节点连左孩子的右孩子、去掉和右孩子的连线。(右孩子变右兄弟)
任一树/森林对应一棵二叉树,二叉树对应唯一的树/森林。森林的先根序列和对应的二叉树先根序列相等,后根序列与对应二叉树的中根序列相等。
加权路径长度WPL:外节点的权值*深度之和。所有扩充二叉树中,WPL最小的称为最优二叉树。
二叉树的重建:中根序列和任意一种序列都可以确定唯一一棵二叉树。
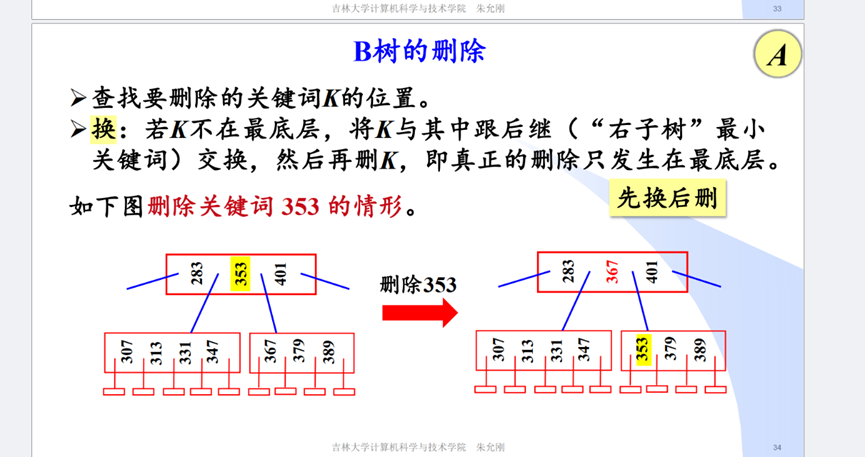
B和B+树
外存访问次数取决于查找树高度。
引入B树的原因:若普通二叉树作为文件系统的索引,随着数据的插入,发现树的深度会变深。而文件系统的索引在磁盘上,磁盘的数据要加载到内存中才能处理,需要反复IO影响查询的效率,于是引入了B树可以作为文件系统的索引。
尽量让B树每个节点大小接近一个磁盘块的大小。
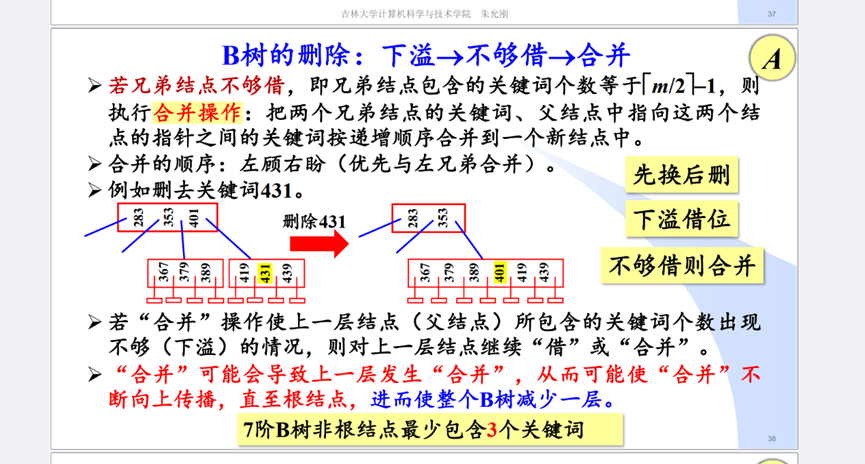
B树是多叉树,一棵m阶B树的性质:每个非根节点最多m-1个关键字,最少ceil(m/2)-1个关键字;最多有m个分叉,最少有ceil(m/2)个分叉;根节点最多m-1个关键字,最少1个关键字;最多有m个分叉,最少有2个分叉。所有的失败结点(叶子节点)都位于同一层,不包含任何信息。B树每个节点可以存放键值和数据。所有结点的平衡因子都为0,叶子结点均在最后一层,倒数第二层称为终端结点。
引入B+树的原因:由于B树每个节点存放数据,而数据相比关键字占用的空间较大,会导致每个磁盘块存放的索引项的记录会变少。B+树的非叶子节点不存放数据,只存放指针和关键字,这样每个磁盘块就可以存放更多的记录。这样深度会减小很多,加快了IO速度。
一棵m 阶的B+树需满足下列条件:每个非根节点最多m个关键字,最少ceil(m/2)个关键字;最多有m个分叉,最少有ceil(m/2)个分叉。根节点最多m个关键字,最少1个关键字;最多有m个分叉,最少有1个分叉。结点的子树个数与关键字个数相等。所有叶结点包含全部关键字及指向相应记录的指针,叶结点中将关键字按大小顺序排列,并且相邻叶结点按大小顺序相互链接起来。所有分支结点(可视为索引的索引)中仅包含它的各个子结点中关键字的最大值及指向其子结点的指针。
在数据库中,B+树常被用作索引结构,用于快速查找和排序大量数据。如主键索引、唯一索引、辅助索引等。在文件系统中,B+树通常用于管理磁盘上的文件块和索引节点。树的高度意味着需要进行多少次I/O操作,高度越少,需要进行的I/O次数相应越少。
简要说说B树和B+树的区别。
B+树的关键码存储的是其对应子结点中关键码的最大值,利用了分块查找的思想,而B树则是利用了二分查找的思想;
m阶B树和B+树:B树的根节点关键字个数取值1到m-1,B+树的根节点关键字取值1到m;B树非根节点关键字取值ceil(m/2)-1到m-1,B+树非根节点关键字取值ceil(m/2)到m。B树分叉个数等于关键字个数+1,B+树分叉个数等于关键字个数。
B树的每个节点既有关键字,又有数据;B+树的数据只在叶子上,非叶子节点只有关键字。
B+树的叶子节点相互之间有一个链路,可以实现范围查找(通过索引结点的索引遍历)。
排序
按规定的顺序,以关键词为依据,对文件内诸多记录进行排列的过程。
关键运算:关键词比较次数、数据移动次数。
稳定性。
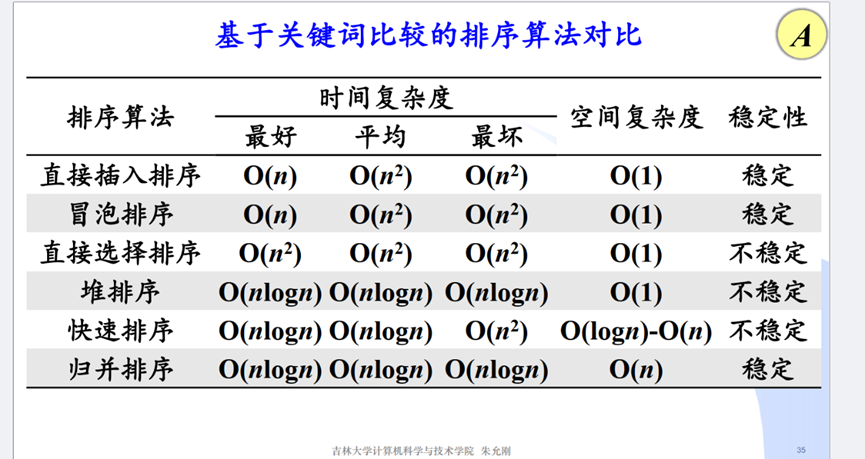
分为内排序、外排序;基于关键词比较的排序、分布排序;平方阶、线性对数阶、线性算法(不依赖关键词比较)。
希尔排序:开始时增量值较大 , 每组中的元素较少 , 插入排序速度较快 ; 随着增量 值逐渐变小 , 大多数元素已基本有序,而插入排序在元素接近有序时速度快。
堆排序:非连续元素访问;归并排序:需要On的额外空间;分布排序:需要更多额外的空间。
归并排序的特点使其非常适用于外部排序,即当排序的数据量太大无法完全加载到内存时,可以通过分阶段地读取和写入数据进行排序。归并排序的时间复杂度始终保持在O(nlogn),无论是最佳、最坏还是平均情况下。
堆:完全二叉树(结构性)、堆序性。
桶排序和计数排序:m个桶或数组长度,时间复杂度O(n+m)。基数排序:O(d(n+r))
快速排序
快速排序之所比较快,因为相比冒泡排序,每次交换是跳跃式的。每次排序的时候设置一个基准点,将小于等于基准点的数全部放到基准点的左边,将大于等于基准点的数全部放到基准点的右边。这样在每次交换的时候就不会像冒泡排序一样每次只能在相邻的数之间进行交换,交换的距离就大的多了。
尽管快速排序在最坏情况下的性能可能较差,但在大多数情况下,它的平均时间复杂度要比归并排序低。相比于归并排序,快速排序的实现更为简洁,代码量更少。
C++ 模板有很强的 inline 优化机制,比较操作相对于赋值(移动)操作要快的多(尤其是元素较大时)。归并排序的比较次数小于快速排序的比较次数,而移动次数一般多于快速排序的移动次数。
归并排序在执行时会将数组分割成多个小块,然后将这些小块递归地排序并合并。尽管分割过程对局部性影响不大,但合并过程需要将数据从不同的内存位置读取并写入临时数组,这种非连续的内存访问模式可能导致较差的缓存性能。
优化:子数组长度≤16时,退出递归,最后进行一次插入排序;递归深度到达logn时,进行堆排序;三数取中(或随机算法,省时且降低最坏情况发生概率);先递归处理短区间,后循环处理长区间(降低空间复杂度为logn)。
查找
顺序查找、对半查找、斐波那契查找、插值查找(假设元素均匀分布,通过线性插值预测mid,平均loglogn,最坏On。缺:但引入了乘除运算,受元素分布影响。应用:先插值查找到一定的范围)。
二叉搜索树、AVL树、红黑树、B树。
哈希函数。
二分缺点:适合有序数组,不适合有序链表;静态查找。
散列
便于快速计算、极少出现冲突(尽可能均匀分布)。以空间换时间,装载因子不应该超过一半。最坏O(n)。且查找失败后,仅能得到关键词不在表中。
拉链法(效率最高,易于删除)、线性探查(很好的空间局部性)、二次/双重探查(避免聚集)。
删除后:考察位置j+1到下一个空位前的元素,是否阻碍查找T[i]。
或用lazy Deletion统计访问次数,删除后按访问次数递减的顺序重新插入。
数组的存储结构
非压缩存储:行优先、列优先;
压缩存储:对称矩阵、上下三角、三对角、稀疏矩阵(三元组、十字链表)。



.jpg)
.jpg)
.jpg)
.jpg)
.jpg)