cs保研经验贴|概率论与数理统计
名词解释
无偏性:估计量的无偏性指的是,估计量的数学期望等于被估计参数的实际值。
一致性:在样本容量逐渐增大的情况下,估计值会越来越接近参数的真实值。
有效性:估计量的有效性指的是最小方差的无偏估计,估计量的方差越小,则该估计量越有效。
概率:对于每一个事件A,有唯一的实数与其对应,且满足非负性,规范性(必然事件=1),可列可加性(两两不相容)。
古典概型:基本事件有限等可能。
伯努利概型:重复n次独立试验,每次实验只有两个可能结果。泊松定理:伯努利实验中稀有事件出现的次数近似满足泊松分布。
离散分布(对应分布律):均匀、0-1、二项(随机变量为事件发生的次数)、几何、泊松。
连续型分布(对应概率密度):均匀分布、正态分布、指数分布。当f(x,y)、fY(y)连续时,可求得X的条件概率密度函数。
数学期望:对于随机变量而言,指的是在其概率意义下的加权平均值。
方差:反映随机变量取值的波动程度,是随机变量与其数学期望差值平方的数学期望
三阶中心矩,偏度,衡量偏离中心的点的位置情况,均值和中位数之间的距离。
四阶中心矩,峰度,衡量偏离中心的点的密集程度。
变量和随机变量:变量是指可变的量,而随机变量的取值不仅可变,还在此基础上对每一个取值赋予了一个取到的概率。
贝叶斯公式:描述了后验概率与先验、似然概率之间的关系,利用先验和似然概率求解后验概率。应用:进行垃圾邮件过滤;通过将病人的先验概率与各种医学测试的似然度相结合,可以计算出某种疾病的后验概率,辅助医生进行诊断和预测。
全概率公式:将对复杂事件的概率转化为在不同情况下发生简单事件的概率的求和。
样本点:对于随机试验,把每一个可能的结果称为样本点。
随机事件:某些样本点的集合。
样本空间(或必然事件):所有样本点构成的集合,记作 Ω。
样本:与总体X有着相同概率分布,且相互独立的随机变量。
试验:满足可重复性、可观测性、随机性。
连续型随机变量的概率密度函数:是描述这个随机变量的输出值,在某个确定的取值点附近的可能性的函数。
泊松分布:常用于对小概率事件进行建模,适合于描述单位时间内随机事件发生的次数。参数λ是单位时间(或单位面积)内随机事件的平均发生次数。
指数分布中,研究随机事件发生间隔,所以对应随机事件的期望是单位时间发生次数的倒数。
卷积:平滑操作、提取图片特征、计算存量。
协方差 cov(X, Y) 定义为两个随机变量X和Y偏离其期望值的乘积的期望,即cov(X,Y) = E[(X - E[X])(Y - E[Y])] 。
大数定律:依概率收敛;当样本数据无限大时,样本均值趋于总体均值,事件 A 发生的频率逼近于它的概率。切比雪夫(独立,有期望有方差,方差有上界,样本均值→总体均值),伯努利(频率→概率),辛钦(独立同分布,有期望可无方差,样本均值→期望)。
依概率收敛:随机变量序列Xn在n很大时,接近常数a。
切比雪夫不等式给出了随机变量与其期望值之间的偏离程度的一个上界。
独立同分布,有期望有方差的中心极限定理:当样本量 n 逐渐趋于无穷大时,n 个抽样样本的均值的频数、多个随机变量的总和(或平均值)逐渐趋于正态分布。
依分布收敛:对于随机变量序列Xn的分布函数Fn(x)的每一个连续点,在n很大时,等于F(x)。
统计量:不含任何未知参数的样本函数。
样本均值和样本方差独立。
点估计:构造出适当的统计量,用其观测值来估计未知参数。
矩估计:根据辛钦大数定律,当样本数足够多时,样本的原点矩收敛于总体的原点矩。步骤:选取k阶矩、计算估计量、解方程。
最大似然估计:概率最大的事件在一次试验中最可能出现。对给定样本观测值的一个关于未知参数的函数:似然函数。
假性检验:提出原假设,选取检验统计量,确定拒绝域,根据样本值计算观测值,对实际问题进行分析,如果发生小概率事件,则拒绝原假设。
三大分布作用:进行区间估计、假性检验时需要避免使用未知的参数,故不同的统计量适用于不同的情况;且相同置信度/显著性水平下,置信度区间长要尽可能小以减小估计误差,拒绝域要尽可能大以覆盖更多极端值,降低第二类错误。 总是控制犯第一类错误的概率不超过显著性水平(小概率事件)。
接受域与置信区间相同。用统计量推断参数时,如果参数未知,则这种推断叫参数估计——用统计量估计未知的参数;如果参数已知(或假设已知),需要利用统计量检验已知的参数是否靠谱,此时的统计推断即为假设检验。
区别:区间估计是根据样本资料去估计总体未知参数的可能范围,假设检验是根据样本资料来检验对总体参数的先验建设是否成立;区间估计立足于大概率,通常以较大的把握(1-a)去估计总体参数的置信区间。而假设检验立足于小概率,通常是给定很小的概率 a 去检验对总体参数的先验假设是否成立。假性检验倾向于接受原假设,即接受明确参数的“真”,而第一类错误就是“弃真”。
正态分布性质:对称性, 唯一峰值,分布范围无界,标准差决定形状,约有99.7%的观测值落在三个标准差范围内。
联合分布的性质:考虑其边缘分布、条件分布。
相互独立:P(XY)、F(XY)、f(XY)
不相关:E(XY)、D(X+Y)

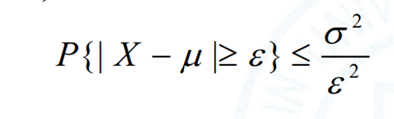

.jpg)
.jpg)
.jpg)
.jpg)
.jpg)