MP有限状态自动机和AC自动机

模式匹配自动机

什么是有限状态自动机？
定义n个不同状态，记为{1,2…n}，在状态i时输入s，达到状态j，记为goto(i,s)=j
对于字符串s而言，在一个状态i下输入一个字符ch，也会达到一个指定状态：
假定新的状态为串s[1,i]+ch的最长相等前后缀，便能够用这个状态机模拟KMP算法匹配字符串的过程。
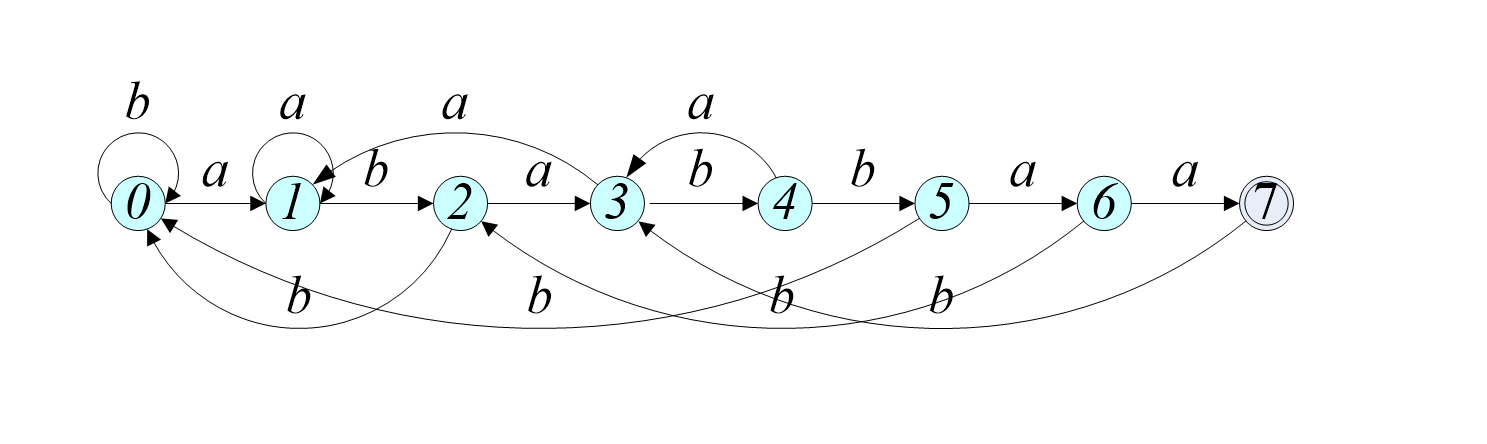
当字符集仅为a、b时，有：
自动机
其中goto(4,a)=3，也就是说abab+a的最长相等前后缀对应的状态是状态3 ，也即表示字符串“aba”的状态。
似乎这样就足够了。
我们获得了goto函数，定义为：

goto(Si,a)：串s[1,i]a的最长相等前后缀。

为了得到这个goto函数的值，我们需要定义fail函数：

fail(Si):串s[1,i]的最长相等前后缀。

因为得到goto(i,a)的前提是，知道s[1,i]的最长相等前后缀s\[1,j] ：若s[j+1]与a相同，则goto(i,a)=j+1，否则求s[1,j]的最长相等前后缀，直到长度为0。
为了表示“s[j+1]与a相同”这一条件，定义函数：

follow(Si, a):状态Si输入a后，来到下一个状态。

对于字符串abcde，follow(0,a)=1,follow(1,b)=2,follow(2,c)=3…以此类推，而其他值未定义。
到这里，goto函数就可表示为：

state go_to(state s,char ch){

    while(follow(s,ch)未定义)
    {
        s=fail[s];
    }
    return follow(s,ch);
}

若s为模式串的状态，ch为s的后继字符，则这一goto值可当做新的fail值。

未定义状态，比如follow(0,b),计为0可不可行？
与之配套地，fail(0),计为0，也就是说空串的最长相等前后缀长度为0。
若fail(0)记为-1，则follow(s==-1,ch)将陷入故障状态：没有状态被记为-1。
问题出现了！函数不得不进入死循环：因为s一直为0。
破环方式也很简单：

引入状态-1，未定义状态记为-1，fail(0)=-1，follow(-1,任何字符)=0。

这样，当计算ab+c的最长相等前后缀时，便能够得到go_to(2,c)=0。
类似地，计算fail的函数为：

Compute_fail()
{
    fail(s0) = ⊥;
    s = s0;
    for( i =1 to |P| ){
        s = goto(s, P[i]);
        fail(si) = s ;
    }
}

goto和fail数组的关系：fail反映模式串中的某部分字符串的最长相等前后缀，goto反映文本串和模式串的匹配情况。诚然，fail数组可以通过goto函数得到，但记录一些中间状态有利于加速算法。
匹配函数为：

Match(t)
{
    s= s0;
    for(int i=1 to |T|){
        if( s 是终止状态 )
           return 匹配!
        else  
            s=goto(s,T[i]);
    }
}

MP有限状态自动机

~~我们都知道mp的c++写法。~~
基于以上定义，我们~~艰难地~~知道mp的有限状态自动机写法：

#include<bits/stdc++.h>
using namespace  std;
#define state int
string P; //模式串
string T;
state fail[1000005];
state edge[1000005][26];

state follow(state s,char ch){
    if(s==-1) return 0;
    if(edge[s][ch-'A']==s+1) return s+1;

     return -1;
}
state go_to(state s,char ch){

    while(follow(s,ch)==-1)
    {
        s=fail[s];
    }
    return follow(s,ch);
}

void get_fail(){
    fail[0]=-1;
    state s_=0;
    for(int i=1;i<P.size();i++){
        s_=go_to(s_,P[i]);
        fail[state(i)]=s_;
        
           if(fail[s_]!=-1&&P[s_+1]-'A'==P[i+1]-'A'){
            fail[state(i)]=fail[s_];
        }//！！！K优化！！！
        
        edge[i-1][P[i] - 'A'] = i;
    }
}
void match(){
    state s_=0;
    for(int i=1;i<T.size();i++){
        s_=go_to(s_,T[i]);
        if(s_==state(P.size()-1)){
            cout<<i-P.size()+2<<endl;

        }
    }
}
signed main() {

    cin>>T>>P;
    P=" "+P;
    T=" "+T;

    get_fail();

    match();

for(int i=1;i<P.size();i++){
    cout<<fail[i]<<" ";
}

}

洛谷提交情况如下：洛谷
这是一种没有任何实战意义的写法。
需要注意俩点：

if(edge[s][ch-‘A’]==s+1) return s+1;

只有计算fail函数时，遍历过某个字符时，才连一条edge边。
也就是说，在未遍历时，字符串abc的follow(0,a)=-1,follow(1,b)=-1,follow(1,c)=-1,而当遍历过b时，follow(0,a)=1,follow(1,b)=2,follow(1,c)=-1。这样做的原因是，若模式串天然有follow边，则fail数组的值会依次为-1,1,2,3,4…

if(fail[s_]!=-1&&P[s_+1]-‘A’==P[i+1]-‘A’){
fail[state(i)]=fail[s_]; }

这是knuth优化。对于字符串aaaa，mp的fail数组是0,1,2,3而kmp的fail数组是0,0,0,3。
因为kmp的fail数组不能很好地反映字符串的前后缀的关系，而我们通常需要利用这种关系，故现常用mp，且把mp称为kmp。

MP算法是一个O(m+n)的算法，证明如下：

1.在check函数中，对文本串扫描一遍，无回头扫描，消耗O(n)
2.自动机向右的移动距离 >= 向左移动的距离>=调用fail的次数，而向右的移动距离= 对文本串扫描的距离=n，故调用fail的次数=O(n)
3.构造fail数组时，向右的移动距离= 对模式串扫描的距离=m，即Fail构造复杂度的复杂度为O(m)

综合为O(m+n)。实际上，除了aaab匹配aaaaaaaa这种极端数据外，mp和暴力算法复杂度接近：随机情况下，暴力的复杂度也接近O(m+n)，在数据随机生成的情况下，暴力匹配也基本很快就会失配。

AC自动机

虽然MP有限状态自动机看起来多此一举，但可以很便捷地理解AC自动机。
AC自动机要完成以下任务，对于一系列字符串t1，t2，t3，判断他们在文本串s中是否出现。
当然，可以跑3次mp算法，但这太过于漫长。
AC自动机需要利用字典树字典树。
建树如下：

void build(int noww){
    int now=0;
    for(int i=0;i<s[noww].size();i++){
        if(AC_[now].a[s[noww][i]-'a']!=0){
            now=AC_[now].a[s[noww][i]-'a'];
        }
        else {
            AC_[now].a[s[noww][i] - 'a'] = ++cnt;
            now=AC_[now].a[s[noww][i]-'a'];
        }
    }
    AC_[now].end.push_back(noww);
}

当我们建立好字典树时，也需要fail数组的值：
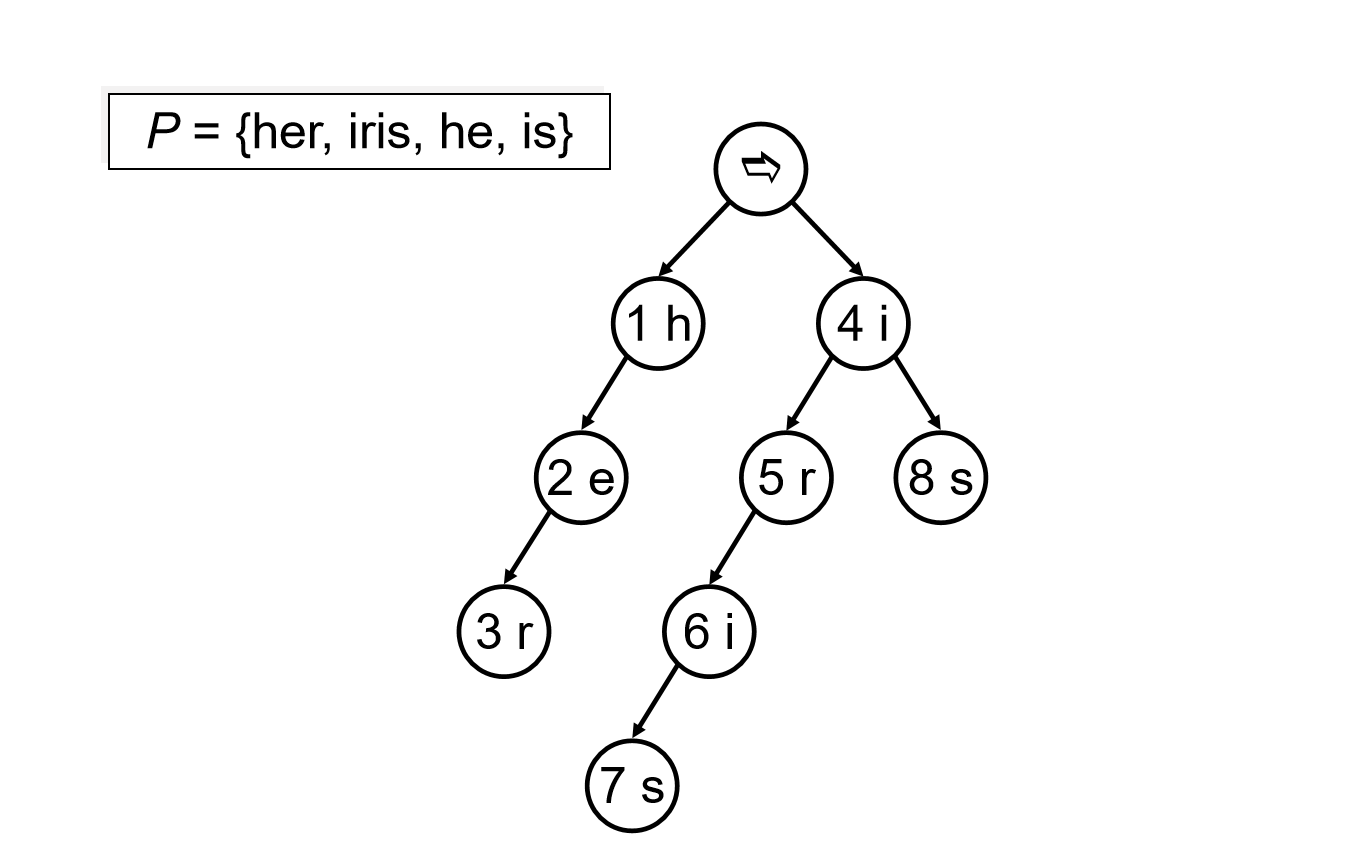
注意：AC自动机的fail数组，其前缀和后缀未必出现在同一模式串上。如：

fail(7)=8,虽然6来自单词iris，4来自单词is。这样做的目的是，当匹配到iris时，也能匹配到可能的模式串is。
这就需要我们打一个标记，来记录“is”是不是模式串。
和上面同样的问题，计算fail就需要利用之前的fail值：

void get_fail(){
    AC_[0].fail=0; //0的fail是0
    queue<int> q;
    for(int i=0;i<26;i++){
        if(AC_[0].a[i]!=0){
            AC_[AC_[0].a[i]].fail=0;  //第一层字母的fail是0，因为不存在最长相等前后缀
            q.push(AC_[0].a[i]);
        }
    }
    //按层由浅到深递增填写fail函数
    while(!q.empty()){
        int iq=q.front();
        q.pop();
        for(int i=0;i<26;i++){
            if(AC_[iq].a[i]!=0){
                AC_[AC_[iq].a[i]].fail=AC_[AC_[iq].fail].a[i]; //只计算一次，就能得到fail函数
                q.push(AC_[iq].a[i]);
            }
            else{
                AC_[iq].a[i]=AC_[AC_[iq].fail].a[i]; //将AC自动机转化为模式匹配自动机，全部字母都对应跳转边，比AC自动机需要更多的空间

            }
        }
    }
}

模式匹配自动机带来的优化:
当文本串是“irisis”时，因为AC_[7].fail=8,goto(8,i)=0,follow(0,i)=4，故新的状态为4。
否则，计算goto(8,i)=0,再计算goto(0,i)=4，就需要经过不止两次goto，而非固定的一次goto。
时间复杂度分析：

AC自动机构造算法时间复杂为 O(|P|)，|P|模式集合中模式的长度之和

模式匹配搜索时间复杂 O(n + occ)，occ为模式出现次数(因为状态需要通过fail函数跳跃)

问题：T=aaaaaaaa，P={a,aa,aaa,aaaa,aaaa}时，搜索复杂度是多少？

check函数如下：

int check(){
    int now=0;
    int ans=0;
    for(int i=0;i<ss.size();i++){
        now=AC_[now].a[ss[i]-'a'];
        for(int j=now;j!=0&&AC_[j].end!=-1;j=AC_[j].fail){
            ans+=AC_[j].end;
            AC_[j].end=-1;  //防止重复计数
        }
    }
    return ans;
}

AC自动机简单版

优化：
使用拓扑排序，不进行fail跳跃(以下check是统计出现了几次，上面check是统计出现了几种)：

void topu(){
    queue<int> q;
    for(int i=1;i<=cnt;i++){
        if(in[i]==0) q.push(i);
    }
    while(!q.empty()){
    int iq=q.front();
    q.pop();
        jishu[AC_[iq].num]+=AC_[iq].ans;
    AC_[AC_[iq].fail].ans+=AC_[iq].ans;
    in[AC_[iq].fail]--;
    if(in[AC_[iq].fail]==0) q.push(AC_[iq].fail);
    }
}

void check(){
    int now=0;

    for(int i=0;i<ss.size();i++){
        now=AC_[now].a[ss[i]-'a'];

            AC_[now].ans++;

    }
    topu();
}

AC自动机

设n为文本长度，k是模式数量，则：
最好匹配次数为n
最坏匹配次数为(1+n)*n/2+n²-nk
AC自动机

比特并行算法

比特并行：一个机器字操作，能对所有比特进行改变。

非确定自动机NFA

MP的非确定自动机：
同一时刻，不只有最长的前缀被匹配，更短的前缀也同时被匹配。
在DFA中，活跃状态只有一个，其他状态通过“后缀链”连接；而NFA中，他们都是活跃状态(空前缀永远是匹配的；每次匹配，都能得到一系列活跃状态的集合(用机器字代表这些集合，机器字的每一个比特代表一个前缀是否匹配))。
NFA中没有必要有后缀链存在，而是只存在向前的链接。

举例：shift-and算法

文本串为ababb，模式串为abab，则状态变化为：

轮次\前缀	a	ab	aba	abab
初始D表	0	0	0	0
输入a后D表	1	0	0	0
输入b后D表	0	1	0	0
输入a后D表	1	0	1	0
输入b后D表	0	1	0	1
输入b后D表	0	0	0	0

形式化：设B[a]表示a在模式串存在的位置，即{1,0,1,0}，B[b]表示b在模式串存在的位置，即{0,1,0,1}，每次变化计为：
$D = (D >> 1) | 1 按位与 B [t_{i}]$
第一次移位得到可能活跃的集合，第二次取交得到活跃的集合。
shift-or：以0代表匹配，1代表不匹配。B[a]表示a不在模式串存在的位置，即{0,1,0,1}，B[b]表示b在模式串存在的位置，即{1,0,1,0}(D向量初始全1)：
$D = (D >> 1) 按位或 B [t_{i}]$

注意：字符串是小端顺序，D、B向量是大端顺序：以上移位都应该向左移位

扩展

比特并行算法能很好地处理通配符匹配问题：

#include<bits/stdc++.h>
using namespace  std;
string P;
string T;
bitset<1000005> B[256];
bitset<1000005> D=0;
int main(){
    cin>>P>>T;
    for(int i=0;i<P.size();i++){
        B[P[i]][i]=1;
        B[(int)'-'][i]=1;
        if(P[i]=='a'||P[i]=='b'){   //-和任意字符匹配，*和a，b匹配：当然，也可以随意指定
            B[(int)'*'][i]=1;
        }
        if(P[i]=='*'){
            B[(int)'a'][i]=B[(int)'b'][i]=1;
        }
        else if(P[i]=='-'){
            for(int j=0;j<256;j++){
                B[j][i]=1;
            }
        }
    }



    for(int i=0;i<T.size();i++){
        D=D<<1;
        D[0]=1;
        D=D&B[T[i]];
        if(D[P.size()-1]==1){
            cout<<"success at "<<i-P.size()+1<<endl;
            return 0;
        }
    }
    cout<<"fail"<<endl;

}

//a-a*cc
//*a-b--
//匹配成功

比较

NFA需要硬件支持并行机制，空间占用小；
DFA只需要串行操作，空间占用大。
参考资料：
1.kmp和mp