BM算法(手算版)
BM算法是一种字符串匹配的算法。
与KMP相比,BM算法不扫描全部输入字符,平均匹配时间c·n, 常量 c <1 (随机或真实文本), 但最坏情况是O(n·m).
可以将BM算法的最坏情况改进到O(n):通过记录文本后缀中最长的模式后缀。
要使用BM算法,需要知道两个信息:
1.用于坏字符规则的bc数组
2.用于好后缀规则的gs数组
坏字符规则分为两种情况:
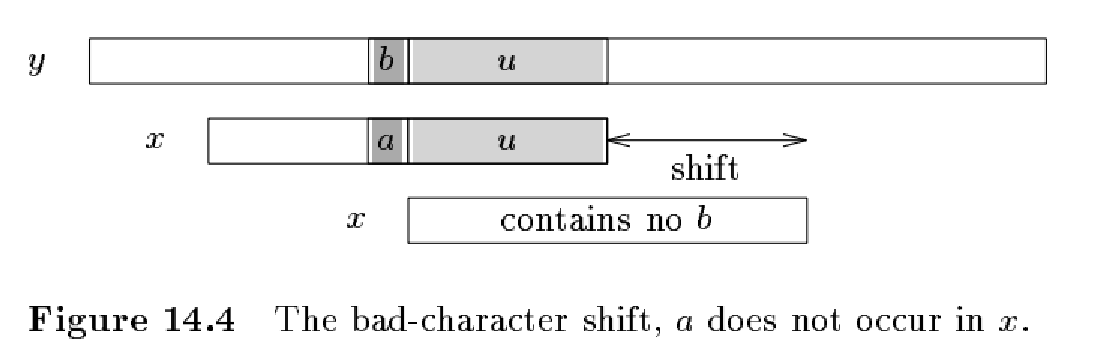
1.失配位置指向的文本串中对应的字符 ,不存在于模式串中。
如上图所示,在这种情况下,直接将整个模式串移动到失配位置 之后。
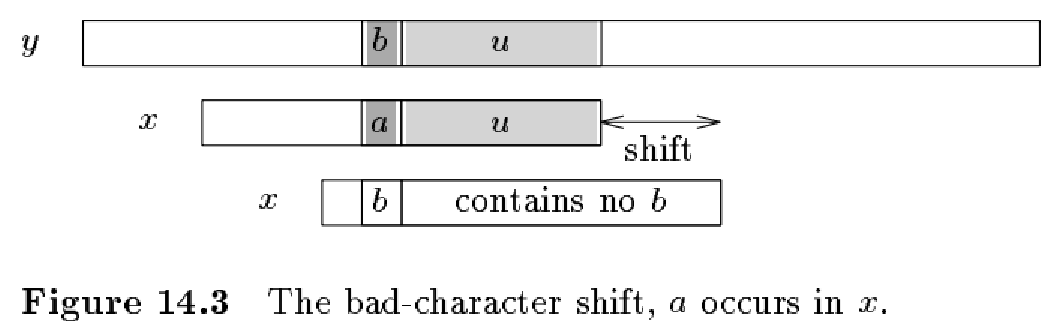
2.失配位置指向的文本串中对应的字符 ,存在于模式串中,且在失配位置 的左边。
如上图所示,在这种情况下,将模式串中的文本串中对应的字符 放在失配位置 上。
需要注意两个问题:
1.这个“模式串中的文本串中对应的字符 ”,是整个模式串从右往左数的第一个符合的字符。否则会造成过度左移。
2.模式串中最后一个字符,不能和任何的失配位置 匹配。这是因为“失配”的前提是有匹配,而右边第一个字符必然被匹配;否则在右边第一个字符失配,那说明所需要的字符不是这个右边的第一个字符。故最后一个字符对应的位置是从右边数第二个符合数的位置。
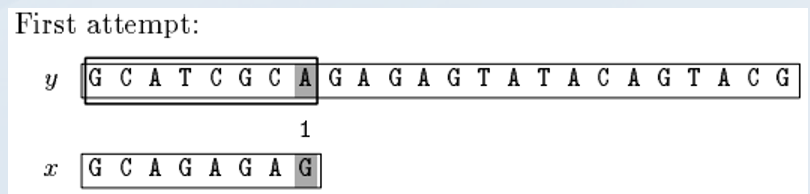
如字符串“GCAGAGAG”的坏字符表为(从0开始计数,从右往左数):
| char | A | C | G | T |
|---|---|---|---|---|
| bc[char] | 1 | 6 | 2 | 8 |
坏字符表不是一直有效的。如果坏字符表中记载的位置,在失配位置 的右边,那么可能会造成负位移或原地不动。
一个解决方法是,记载每次失配位置 的左边的第一个符合的字符:但这很麻烦。
这并不是说位移就是上表的值。位移= bc[char]-失配位置Z。(从右往左数,0开始)
好后缀规则分为3种情况:
rule3:
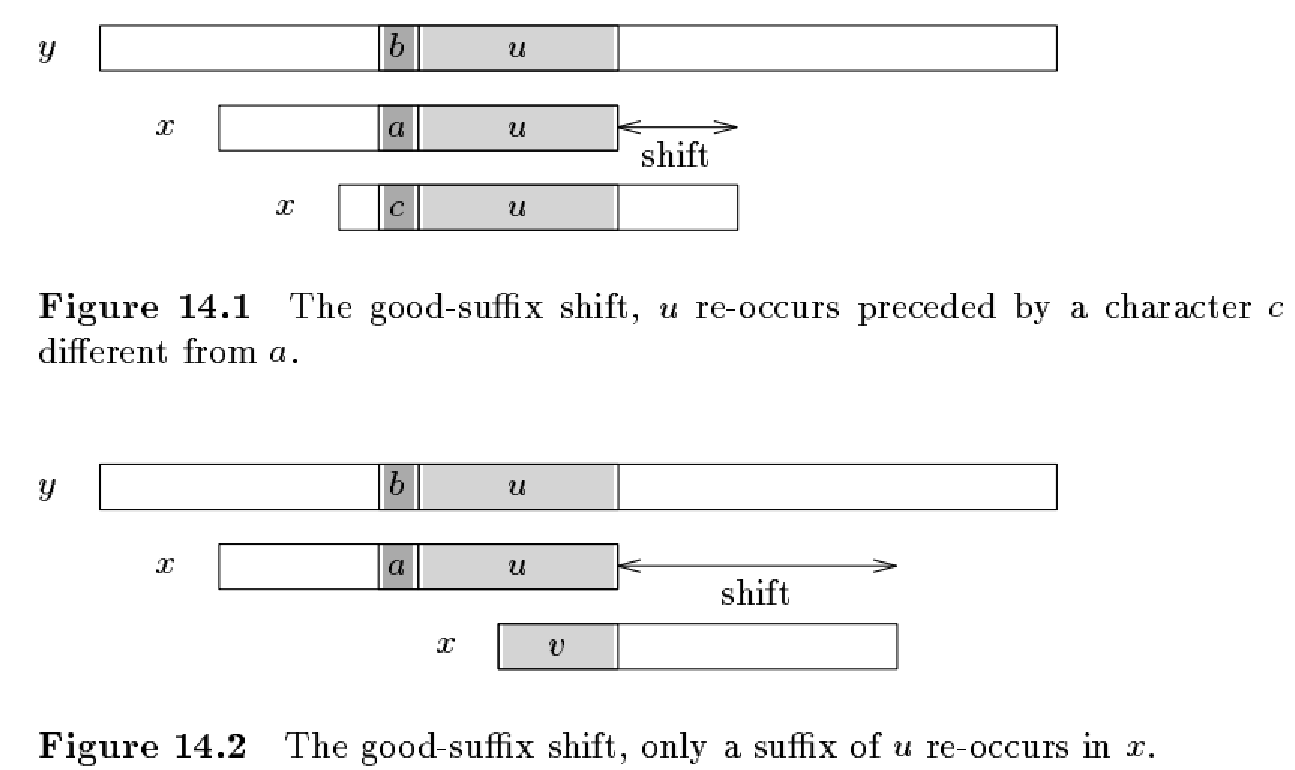
如图14.1,目前匹配好的后缀u,在模式串中存在。如果有多个,则取最靠右的且c!=a的那个,并将其对齐。
rule2:
如图14.2,目前匹配的好后缀u,在模式串中其他位置不存在。但它的后缀,和模式串的前缀相同。如果有多个满足的后缀,则取最长的那个后缀,并将其对齐。
rule1:
如图14.?,目前匹配的好后缀u,在模式串中其他位置不存在。且它的每一个后缀,和模式串的前缀都不相同。这种情况下,直接将整个模式串移动到当前的最右端之后。
好后缀规则和坏字符规则是可以同时使用的,我们每次取俩者中最大的那个。
如坏字符规则一样,好后缀也有自己的表,叫做gs数组。要想得到gs数组,首先要利用suff数组。
suff数组:存储从字符s[i]向左开始计数的,和模式串最右边字符开始的匹配的字符个数。
如字符串“GCAGAGAG”的suff为(从0开始计数):
| G | C | A | G | A | G | A | G |
|---|---|---|---|---|---|---|---|
| 1 | 0 | 0 | 2 | 0 | 4 | 0 | 8 |
从右往左看:
从G开始,GAGAGACG与GAGAAGACG匹配,个数是8,故填8。
从A开始,没有字符匹配(因为右边第一个字符是G),故填0。
从G开始,GAGA(下一个是C)与GAGA(下一个是G)匹配,个数是4,故填4。
从A开始,没有字符匹配(因为右边第一个字符是G),故填0。
从G开始,GA(下一个是C)与GA(下一个是G)匹配,个数是2,故填2。
从A开始,没有字符匹配(因为右边第一个字符是G),故填0。
从C开始,没有字符匹配(因为右边第一个字符是G),故填0。
从G开始,G(下一个是末尾)与G(下一个是A)匹配,个数是1,故填1。
接下来,我们依次处理rule1,rule2,rule3,来获得gs数组。
为什么是这个顺序:因为rule1位移>rule2位移>rule3位移,大的值被小的值取代,才不会造成过度右移。
具体的理解,可以见高效字符串匹配算法
施加rule1:
所有的项均有最大位移8(字符串长):
| G | C | A | G | A | G | A | G |
|---|---|---|---|---|---|---|---|
| 8 | 8 | 8 | 8 | 8 | 8 | 8 | 8 |
施加rule2:
step1:从右往左扫描模式串,找到第一个下标(下标从左往右数,从0开始计。略过最右边的数)+1=suff[i]的位置。对上面的例子来说,这个位置是“i=0”,对应的是最左边的字符G。
step2:从左往右扫描字符串,将扫描过的位置对应的gs数组改为“当前值-suff[i]”,直到剩下suff[i]个字符。
step3:step继续向左,step2继续向右,直到扫描完成。
| G | C | A | G | A | G | A | G |
|---|---|---|---|---|---|---|---|
| 7 | 7 | 7 | 7 | 7 | 7 | 7 | 8 |
施加rule3:
从左往右扫描字符串(略过最右边那个),将gs[suff[i]]改为i(下标从右往左数,以0开始):
变化1:
| G | C | A | G | A | G | A | G |
|---|---|---|---|---|---|---|---|
| 7 | 7 | 7 | 7 | 7 | 7 | 7 | 8 |
变化2:
| G | C | A | G | A | G | A | G |
|---|---|---|---|---|---|---|---|
| 7 | 7 | 7 | 7 | 7 | 4 | 7 | 5 |
变化3:
| G | C | A | G | A | G | A | G |
|---|---|---|---|---|---|---|---|
| 7 | 7 | 7 | 2 | 7 | 4 | 7 | 3 |
变化4:
| G | C | A | G | A | G | A | G |
|---|---|---|---|---|---|---|---|
| i=0 | i=1 | i=2 | i=3 | i=4 | i=5 | i=6 | i=7 |
| 7 | 7 | 7 | 2 | 7 | 4 | 7 | 1 |
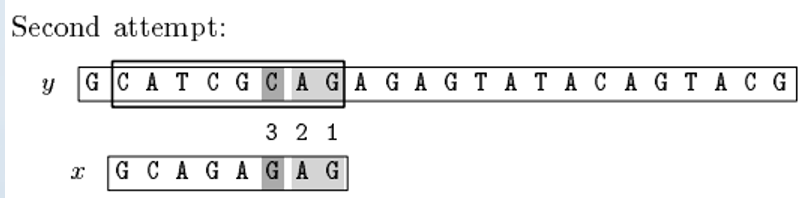
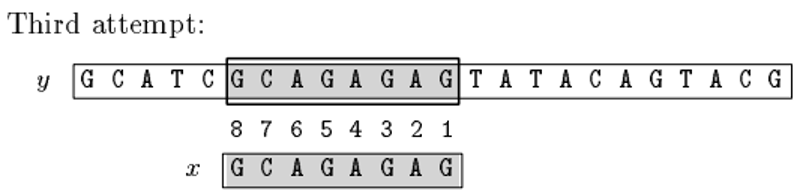
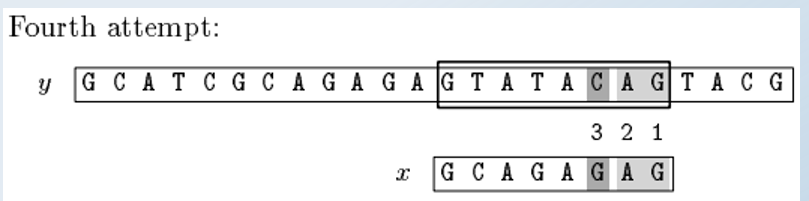
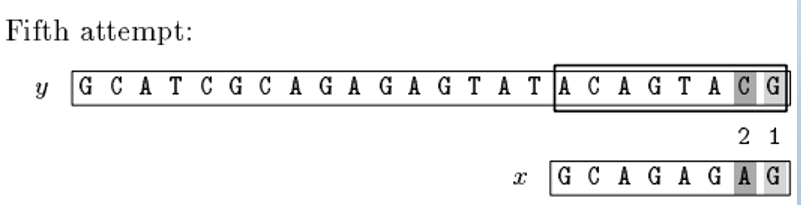
向右位移=max(bc[A]-Z,gs[7])=max(1-0,1)=1;
向右位移=max(bc[C]-Z,gs[5])=max(6-2,4)=4;
向右位移=max(0,gs[-1---->0] )=max(0,7)=7;
向右位移=max(bc[C]-Z,gs[5])=max(6-2,4)=4;
向右位移=max(bc[C]-Z,gs[6])=max(6-1,7)=7;
附:对于字符串aaaaaa,其gs数组为{6,6,6,6,6,6}—>{1,2,3,4,5,6}—–>{1,2,3,4,5,6}。
1.KMP算法的实际性能不好,一般实际中不用
2.BM速度快,但最快的BM类算法不是完整BM算法而是简化的版本(复杂度和效率的折中版本)
若模式串长为m,文本串长为n:
BM算法最好情况下比较m次,最坏情况下比较(n-m+1)*m次
MP算法最好情况下比较m次,最坏情况下比较(n-m+1)*m次
平均比较次数:?
参考内容:
1.BM-c++