判断题

1.正确

桥的两端应该为主体，桥中可包含主体和客体

2.错误

如果明文本身就是对称的，则密文有可能相同

3.错误

bad character表只记录某个字符从右往左最先出现的位置，并不记录所有字符的位置

4.错误

HRU模型只能用and连接条件命令，不存在or

5.正确

dom关系是一种偏序关系，偏序关系具有传递性

6.正确

误报率和检测率不存在确切关联

7.正确

该程序设置了suid，且创建者是root，则用户运行时拥有超级用户权限

8.正确

图灵机停机问题可规约为可靠性问题，解决可靠性问题可解决图灵机问题，图灵机问题不可解则可靠性问题不可解

9.正确

采用low-water-mark策略时，主体的完整性=min(主体的完整性，所读客体的完整性)

10.正确(?)

角色的互斥关系可以实现职责分离

填空题

1.0,50%
2.n(n+1)/2+n²-nk
3.0
4.略
5.1340415(?)

分析、计算、证明题

第1题

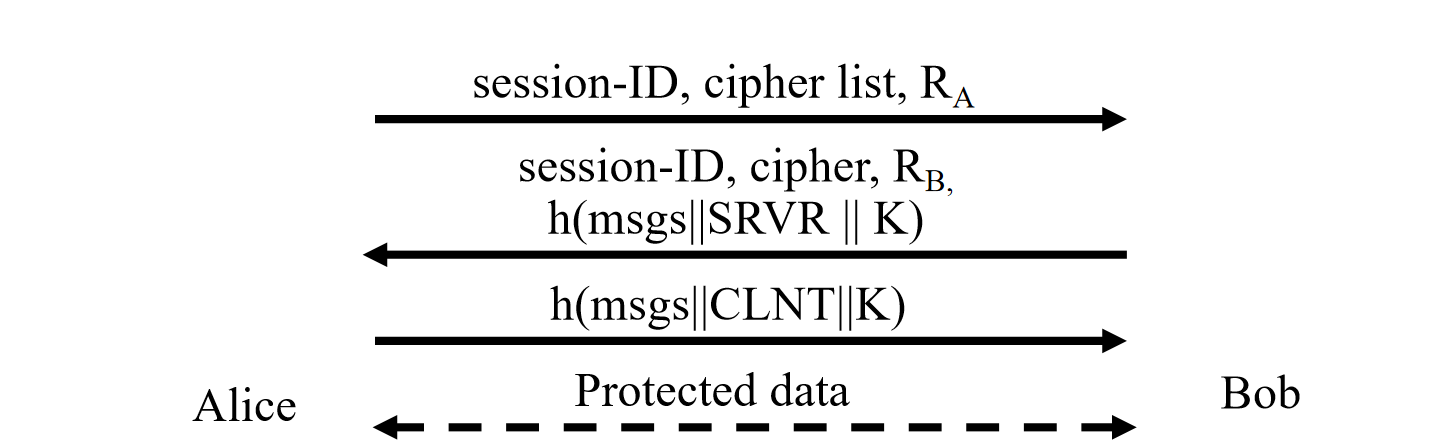
会话建立：
协议
连接建立：
协议
通讯：会话需要四次交互，而连接只需要三次交互(?)
计算复杂性：会话建立使用了公钥算法，计算复杂性高，连接建立未使用公钥算法

第2题

自然语言描述：用byte指针first指向A[0]的第一个字节，用byte指针last指向A[1]的最后一个字节，交换内容后first指针后移，last指针前移，重复8次
时间复杂度：一共需要交换8次，每次交换能在O(1)时间完成，故时间复杂度为O(w)，w为字节的个数
在reverse函数中填写代码，最终输出16,15,14,13…2,1

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
#include<bits/stdc++.h>
using namespace  std;
bitset<64> b[2];

    void reverse()
{
    byte* first=(byte*)&b[0];
    byte* last=(byte*)&b[2];
    last--;
     for(int i=1;i<=8;i++){
         byte tmp=*first;
         *first=*last;
         *last=tmp;
        first++;
        last--;
     }

}
void reverse2(){
        auto *it=(bitset<128>*)b;
        bitset<128> tmp1("00000000111111110000000011111111000000001111111100000000111111110000000011111111000000001111111100000000111111110000000011111111");
        bitset<128> tmp2("11111111000000001111111100000000111111110000000011111111000000001111111100000000111111110000000011111111000000001111111100000000");
        *it=((*it&tmp1)<<8)|((*it&tmp2)>>8);
        bitset<128> tmp3("00000000000000001111111111111111000000000000000011111111111111110000000000000000111111111111111100000000000000001111111111111111");
        bitset<128> tmp4("11111111111111110000000000000000111111111111111100000000000000001111111111111111000000000000000011111111111111110000000000000000");
        *it=((*it&tmp3)<<16)|((*it&tmp4)>>16);
        bitset<128> tmp5("00000000000000000000000000000000111111111111111111111111111111110000000000000000000000000000000011111111111111111111111111111111");
        bitset<128> tmp6("11111111111111111111111111111111000000000000000000000000000000001111111111111111111111111111111100000000000000000000000000000000");
        *it=((*it&tmp5)<<32)|((*it&tmp6)>>32);
        bitset<128> tmp7("00000000000000000000000000000000000000000000000000000000000000001111111111111111111111111111111111111111111111111111111111111111");
        bitset<128> tmp8("11111111111111111111111111111111111111111111111111111111111111110000000000000000000000000000000000000000000000000000000000000000");
        *it=((*it&tmp7)<<64)|((*it&tmp8)>>64);
    }

signed main() {
        ios::sync_with_stdio(false);
        cin.tie(nullptr);
        cout.tie(nullptr);
     for(int i=1;i<=16;i++){
       bitset<8> tmp=bitset<8>(i);
       for(int j=0;j<8;j++){
           b[0][(i-1)*8+j]=tmp[j];
       }

     }
    reverse2();

    for(int i=1;i<=16;i++){
        bitset<8> tmp;
        for(int j=0;j<8;j++){
           tmp[j]= b[0][(i-1)*8+j];
        }
        cout<<tmp.to_string()<<endl;

    }

}

第3题

ff(1)=2*(x-2)(x-4)/(1-2)(1-4)=10(x-2)(x-4);
ff(2)=1(x-1)(x-4)/(2-1)(2-4)=3(x-1)(x-4);
ff(3)=5(x-1)(x-2)/(4-1)(4-2)=30(x-1)*(x-2);
相加得：x²-4x+5(mod 7)

第4题

由于未给出U值，而计算U值需要(b)的结果，故先用高精度算法计算(b):
转化为 1/100 mod 71
R=100,b=10,m=71,m’=-m^(-1)mod 10=9，且满足条件gcd(m,b)=1,m<R,T/m<R
由于100=10²，故需执行2次：
step0:
u0=T0*m’ mod 10=1*9 mod 10=9
T=T+u0*m*1=1+9*71*1=640
step1:
u1=T1*m’ mod 10=4*9 mod 10=6
T=T+u1*m*100=640+6*71*10=4900
step3:
T=T/R=49(<100)
故(b)=69，即m’=69
(a):
x=MR(17*(R² mod 71))=67
MR(x²)=MR(67*67 mod 71)=3
MR(x²²)=MR(3*3 mod 71)=15
MR(67*15 mod 71)=42
MR(42 mod 71)=70

第5题

设两个矩阵分别为A={a,b,c,d},B={a’,b’,c’,d’},则：
PMul((a,b,0,c,d),(c’,a’,0,d’,b’))的7次项为aa’+bc’,1次项为cb’+dd’，
PMul((a,b,0,c,d),(d’,b’,0,c’,a’))的7次项为ab’+bd’,1次项为ca’+dc’，
共使用两次得到结果。

第6题

因为A不知道k，故无法计算出ri，即A无法知道i，实现了(i);
因为B知道r0和r1的差值，故B能通过将另一个mi’减掉这个差值得到mi’，未实现(ii);
因为其他人不知道k，故无法计算出ri，也无法计算出mi，故实现了(iii)
修正：
B将k用A的公钥加密后，计算出r再发给A，A收到且计算出k0和k1后进行解密，再计算m0’和m1‘发给B