计算机安全:快速比特操纵算法
使用机器字操作(算术、逻辑运算)实现机器字中的比特的计算和变换,是一种时间复杂度与机器字长无关的算法。
1 | unsigned int v; //c的值即1的个数 |
分块和
对于一个二进制数x(总位数为w),将其划分为多段相同长度u的区间,将每个区间内的1的个数转化为二进制,首尾相接得到y:y称为x的u分块和。
例如:101010的1分块和是1,0,1,0,1,0,101010的2分块和是01,01,01,101010的6分块和是000011。
因为u位能表示的最大个数,大于等于u的长度,故该方式能正确表达出分块和而不发生溢出。
递推表达式
说明
简单来说,便是将奇数个u区间和偶数个u区间相加。
例如上面01010101的例子:
先将01010101和00110011按位与,只保留奇数位u区间得到00010001;
再将01010101右移u位,得到00010101,与00110011按位与,只保留偶数个u区间得到00010001。
再将两数相加,完成合并。
这种方法参照了递归方式,计算1的个数的时间复杂度是O(log w),小于上一方法的O(w)。
特例
若一个数,每个区间除了最后一位为0/1,其他位都为0:换而言之,最低位的数表示这个u区间有多少个1:
形如001001001001、000000001001,将其与001001001001相乘,结果的从右往左数的第m-1=w/u-1(从0开始计数)个u区间的值为此二进制数的1的个数。
对于这个例子,001001001001与001001001001相乘,结果为1010011100011010001,得到001001001001中1的个数是4。
推广
即:通过移位和按位与,强制将每一部分的数变成“每个区间除了最后一位为0/1,其他位都为0”的形式。
如110110,分块为110,110,求第0,1,2位的1的个数的操作分别为000000*001001,001001*001001,001001*001001。
将上面的结果相加,取从右往左数的第w/u-1(从0开始计数)个u区间的值,便是110110中1的个数,得到4。注意:分块长度至少为lgw,否则相加时会产生进位(即需满足w<2^{u})。
总结:如果设区间长度为lgw,则需要做[0,lgw)次乘法,并将乘法得到的结果相加,最后取第m-1(从0开始计数)个u区间的值。
加法方法进行到区间长度 u = lgw 时;
用一次乘法,结果的第 m - 1 个 u 区间的值等于 x 中 1 的个数。
时间复杂 O(loglog w)
此时虽然y的每个分块不满足“每个区间除了最后一位为0/1,其他位都为0”,但满足“表示的数的大小为x的对应分块的1的个数”。即结果的第 m - 1 个 u 区间的值并非为y中1的个数,而是x的1的个数。
额外的:
例子:
0001001010001111,分块为4,则x[lgw]为0001,0001,0001,0100(十进制为4372)。
其乘以0001000100010001的结果的第3个数为0111,值为7。同时,4372模15的值也为7。
前导知识
log*(n)的定义:满足log( log( ··· log(n) ··· ) ) <1 的最小log个数。
lg*(32) = lg*(64) = lg*(128) = ··· = lg*(2^16) = 4
u个比特能表示2的u次方-1大小,也即(2的u次方-1)/u个u区间的1的个数之和。
思想:让每次乘法尽最大可能扩张区间长度。
解决
说明:从L(i)区间开始,每次将区间放大为原来的2次幂倍,直到区间长度为lgw。此时运用一次分块乘法,便能得到结果。
原理:存在y,x[u] * y = z,对于 z 的每个u’区间,其最高 u 比特的值是x[ u’]对应区间的值。通过移位等处理,可得到x [u’]
具体公式课堂略过
前导知识
二元de Bruijn序列是一种特殊的周期为2的n次方的序列,满足任意一个二元n长向量都在de Brujn序列的一个周期中恰出现一次。
如n取3时,序列为0001011100,也即00010111的循环:其中000,001,010,011,100,101,110,111只出现了一次。
构造方法
构造哈希函数h(x):其中x是2的幂次方,最大值小于2的w次方,h(x)为0到w-1的任意一个数。
h(x) =B * x >> (w – lg w),lgw整除w(why?)。
这个操作相当于对B进行移位后取高lgw(即上文中的n)位,因为B的特殊性,所以h(x)和x是一一对应的。
构造表D:对于长度为lgw的数(或者说0<=x<w)x,找到lgw维de Bruijn的第x位,取lgw个,得到的数记为y,D[y]=x。(y互不相同;O(w)时间,O(wlgw)空间)
这一步实际上就是由x确定h(x),不同的是,这里的x是LSB的值,而上文的的x是2的幂次方。h(x)的作用是,作为枢纽,连接这两个值。
将word的除了最低置位bit之外的bit置 0(一个方式:(~word+1) AND word,~即按位取反)
结果与De Bruijn序列相乘,取乘积的前lgw bit得到数x’(这一步实际上就是进行h(x))
用结果查表D,得到D[x’],即为LSB的位置
原理
LSB的值根据de Bruijn序列,映射成了唯一的长度为lgw的值,而这长度为lgw的值又通过de Bruijn序列映射成了唯一的2的幂次方。当de Bruijn序列确定时,这两个映射关系是唯一确定的。
构造方法
将 x分为 u bit区间。
将LSB隔离出来,其他bit都是0。(一个方式:(~word+1) AND word,~即按位取反)
注意:其中 u 应该大于根号w,否则做乘法时,00..1串无法覆盖所有的u区间。
计算LSB所在的区间号i
生成一个机器字
原理
LSB后面的所有u区间的最低位为1,故在LSB及其后面有多少个u区间,便有多少个1被加。注意:这里的01串的重复次数是u,而非w/u
计算LSB在区间中的位置j
将x的i区间复制成u份:
只将第j个u区间保留下来:
采用计算区间号i的方法,得到j
则y = u*(i-1)+j。
例子:
100(u为3):
计算i:(0111&(001001001))*(001001001)=001001001,取高u位,即i=1。
计算j:100复制三次:100100100,再与上000100010001得100000000,利用计算i的方法,得到j=3。
最终:(1-1)*3+3=3。
反例:
100 000 000 000…(u为3):
此时不管后面有多少个000,最后都会得到LSB在第三个区间,而这是错误的。那为什么不动态改变机器字F来使得其正确:耗时。
前导知识
SetR(x,u)
此操作根据机器字x中u区间是否为0对u区间进行设置,如果为0,则u区间不变,否则最低位置为1。
反向聚合操作compr(x,u)
此操作将每个区间的最后一个比特聚合在一个u区间中,但顺序相反。
扩散操作diffu(x,u)
此操作将一个u区间的每个比特放置到每个u区间的最低比特上,顺序不变。
计算方法
首先计算MSB所在的u区间的号
(1)y = SetR(x)
(2)y = Compr(y,u)
(3)y = diffu(y,u)
(4)计算y中的MSB的位置 i,因此MSB在x中所在区间为 i’= u-i
计算i’区间中MSB位置
(5)y = x>>(i’u)
(6)y = diffu(y,u)
(7)计算y中的MSB的位置 j,因此MSB所在区间为 j’= u-j
最终可得到MSB的位置为 i’u+j’
此部分在课堂略过
递归方法实现完全比特反转O(lgw)
1 | unsigned int reverse(unsigned int x) |
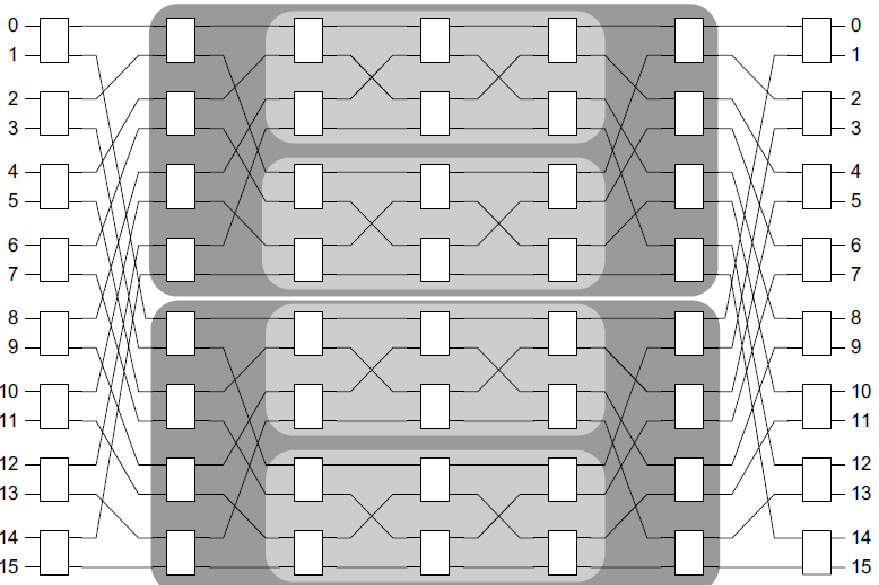
Benes置换网络
可实现任意置换,只需在方块中填写交叉或直连(X或=)。
输入个数是2的幂次方,该置换网络使用多个 2*2 基本交换单元实现置换,输出也为2的幂次方个元素的序列。
BN网络运用了递归的思想,即相邻(奇偶性不同)的输入,分别前往两组,而在某一组中,又再进行分组;而在输出时,每两个输出合并到一个输出,直到两个输出合并成最终输出,完成置换过程。
所需层数:2lgw-1。时间复杂度:O(lgw),空间复杂度:O(lgw)(记录直连还是交换)
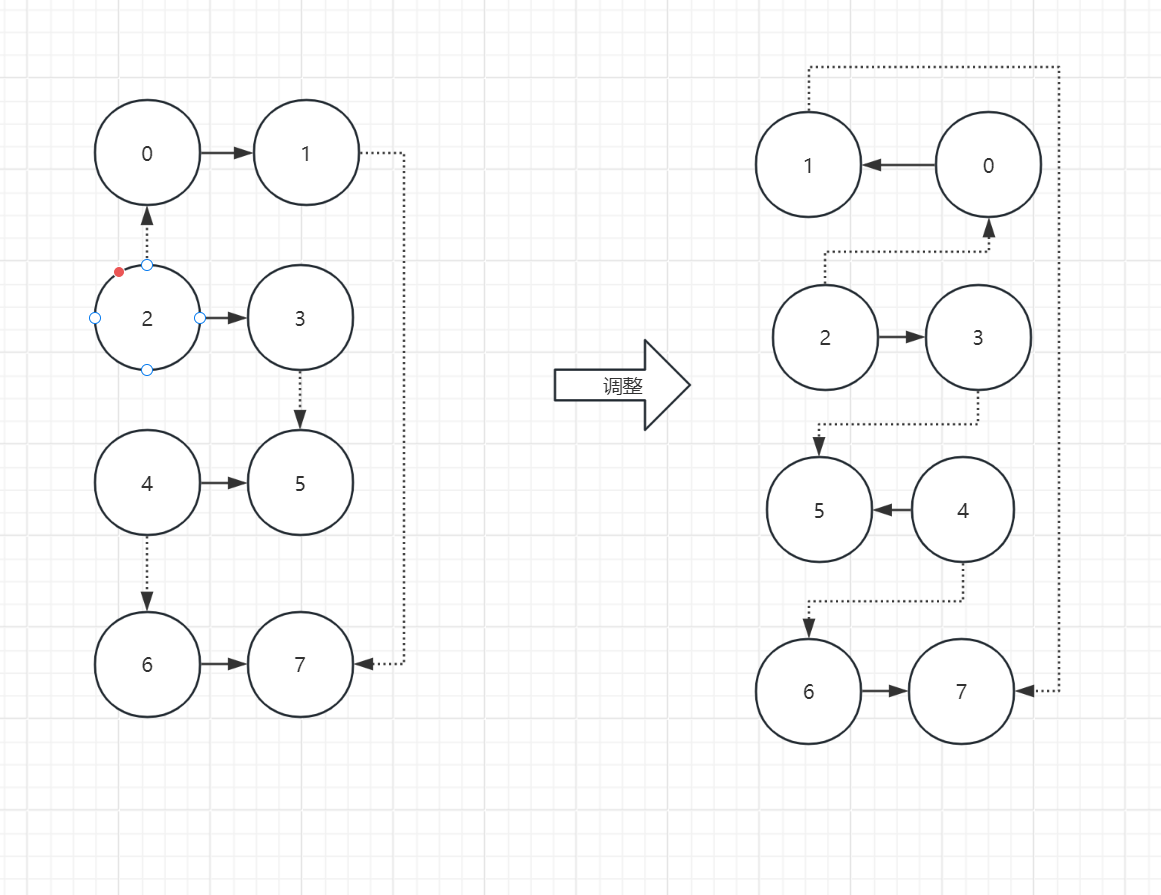
断点图
输入中的相邻用实线连接,输出中的相邻用虚线连接。(作图为俩列)
调整断点图:交换相邻点的位置,使得虚线相连的两个数不在同一列。
获得输入符号:如果一组相邻点换序,则为“×”,否则为“=”。
获得输出符号:在输出中如果一组相邻点为上下关系,在断点图中不为左右关系,则为“×”,否则为“=”。
重复以上过程,直到所有空填上。
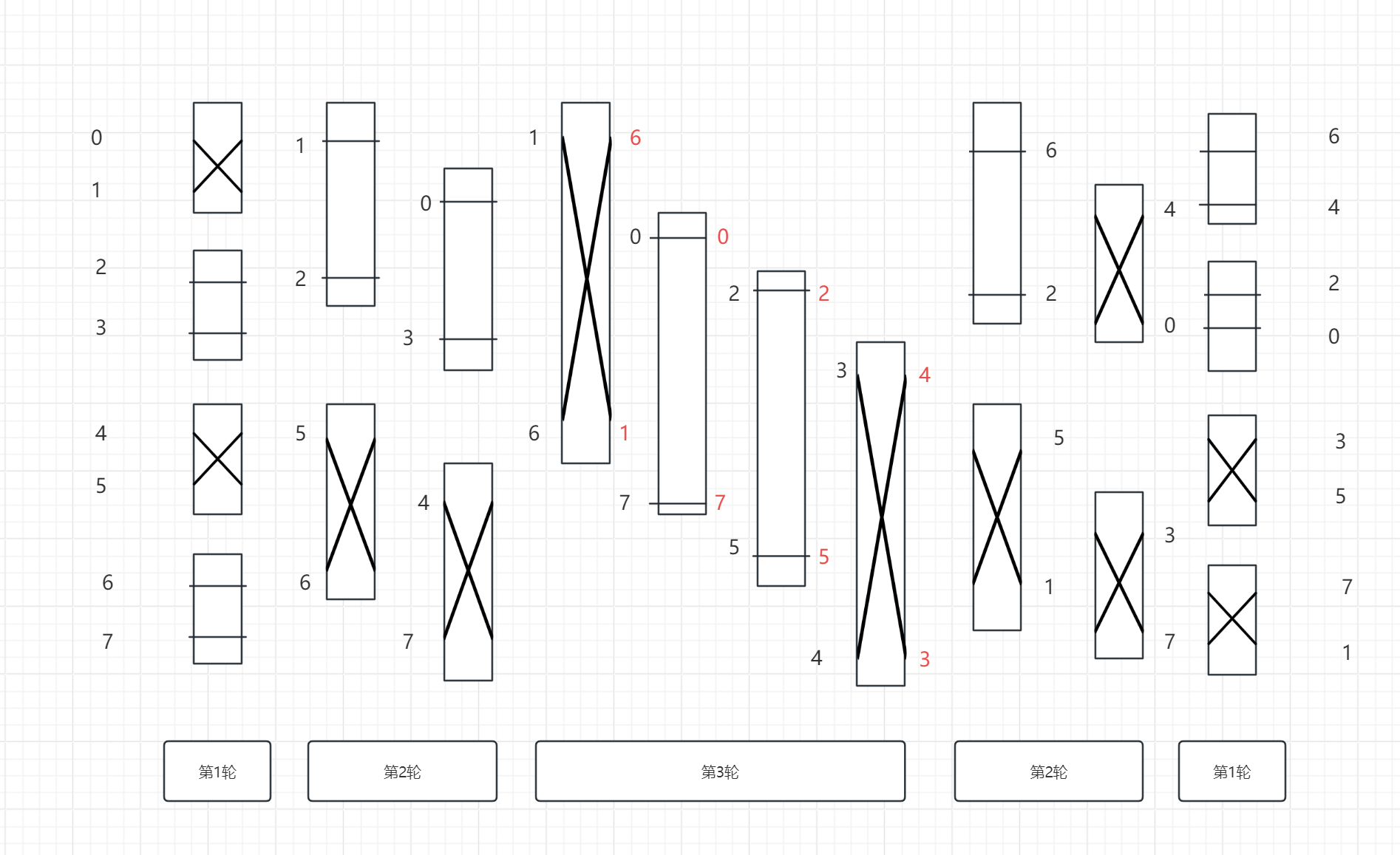
例子:
输入从上到下是01234567,输出从上到下是64203571,(初始输入分组是01/23/45/67,初始输出分组是64/20/35/71。)则作图如下:
输入符号从上到下为“x=x=”,输出符号从上到下为“==xx”。进一步地,获得新的分组。
对输出符号的解释:64是一组且在输出分组中6在上4在下,在输入的调整后的断点图中6在左4在右,故不交换;71是一组且在输出分组中7在上1在下,在输入的调整后的断点图中7在右而1在左,故交换。
断点图实例
注意:线条在方块“背面”经过,意为不进入这一置换单元。
试着将以上例子对应的符号填入方块中。得到:
一般情况m置换单元
输入、输出按顺序分为m个块,每块k个元素。
将每块中的元素分到k个不同组中,使得每组中元素属于输入的不同块。
归结为K正规图着色问题。(why?)
此部分课堂略过
参考资料:
【位操作笔记】详解一种高效位反转算法